THE REBALANCING BONUS:

ABSTRACT

The actual return of a rebalanced portfolio usually exceeds the expected return calculated from the weighted sum of the component expected returns. A formula for estimating this excess return is derived and tested. It is demonstrated that assets with high volatility and low correlation with the remainder of the portfolio provide considerable excess return, or "rebalancing bonus."

Let's assume that you have decided that your desired portfolio composition consists of 50% S&P 500 stocks and 50% long term US treasury bonds. (If you've gotten this far in this website you probably already know that this is a fairly undesirable mix; it merely serves as a good example.) As these two assets frequently move in different directions, the portfolio will eventually drift from the desired 50/50 mix. If you desire to maintain the 50/50 composition, some of the better performing asset must be sold, and exchanged for a similar amount of the more poorly performing asset. This is known as portfolio rebalancing. An understanding of the mechanics of rebalancing is fundamental to sound portfolio management, and yet surprisingly little theoretical attention has been paid to this area. Three important questions concerning rebalancing arise:

1. Should rebalancing be done at fixed regular intervals ("periodically"), versus whenever the asset mix gets out of kilter by a certain amount ("threshold rebalancing")?

2. If done periodically, what is is the optimum interval (i.e., monthly versus quarterly versus annually)?

3. Is there a way to predict how much extra return is available from rebalancing, and is it possible to identify assets which provide superior rebalancing benefit?

For example, Markowitz¹ considers the return of a portfolio to be equal to the weighted sums of the individual component returns, but this formulation is valid only for nonrebalanced portfolios over single periods. It is surprising that Markowitz considered portfolio return to be the weighted sum of the component returns, since he pioneered the idea that portfolio variance, or risk, is not the weighted sum of the individual component variances. In Portfolio Selection he presented Monte Carlo simulations in which the actual returns were significantly higher than the arithmetically derived expected returns, but did not comment on the discrepancy.

A simple, well known example will suffice: The return on common stock for the period 1926-94 was 10.19%, and for long term corporate bonds over the same period 5.51%.⁵ The "Markowitz return" on an equal mixture of the two is the arithmetic mean, or 7.85%. Rebalancing this portfolio on an annual basis to maintain a 50/50 mixture yields a return of 8.34%; a "rebalancing bonus" of 0.49% is realized over the Markowitz return. In fact, however, if one had put equal amounts of money into stocks and bonds on January 1, 1926, and had not rebalanced or paid taxes, then the long term return would have been 9.17%. In this instance the nonrebalanced portfolio has a higher return than the rebalanced portfolio. This is because over the 69 year period studied the significantly higher stock return overwhelms the bond return; for the last 40 years of the period the unrebalanced portfolio consists of greater than 90% stock. Thus the higher return of the unrebalanced portfolio comes at the cost of a much higher risk than the rebalanced one. Perold and Sharpe² point out that rebalancing is a "concave" strategy. Portfolio insurance represents the opposite of rebalancing, and is referred to as a "convex" strategy. They suggest that convex portfolio insurance strategies as well as buy and hold ("flat") strategies produce superior returns in markets with a prolonged upward (or downward) bias, and concave rebalancing strategies produce superior returns in stagnant markets. If the only two assets considered are stocks and bonds, and if stock returns are always higher than bond returns over long time horizons, then obviously buy and hold, as well as portfolio insurance, will produce returns superior to rebalancing. As already pointed out, this will come at the cost of gradually increasing portfolio risk. However, things are very different when looking at global equity portfolios. Over very long time horizons there is usually relatively little difference in the returns in most national equity markets; under such circumstances rebalanced portfolios dominate. For example, when looking at the 1970-94 period, rebalancing various asset pairs almost always provides returns superior to nonrebalanced porfolios. Only when long term return differences among asssets exceed 5 percent do nonrebalanced portfolios provide superior returns, and then only at the cost of increased risk. (The exceptions which prove the rule are the very high returns of Japanese equity, and the very low returns of Australian and Italian equity.) Care should be taken to note that the superiority of rebalancing as a long term strategy pertains only to national and regional markets as a whole, and not among different industry groups. Over the course of decades entire industries often shrivel while others prosper mightily; rebalancing the pharmacutecal and petroleum segments of the S&P500 over the past three decades would have been a disastrous strategy. Although enitre national markets occasionally disappear throught war or nationalization, this occcurs much less frequently than the ongoing remolding of market segment capitalization characteristic of a market economy.

ESTIMATING THE REBALANCING BONUS

A small thought experiment is in order. Let us postulate a portfolio composed of equal parts of two assets, A and B. Further assume that each has a return of either +30% or -10%, with equal probability, and that the portfolio is rebalanced to 50/50 at the end of each year. The long term return of each asset is 8.1665% when annually compounded, and its standard deviation 20%. If the annual returns are perfectly correlated (i.e., r =1) then the equal mixture of A and B will have the same risk and return as each individual asset, and no gain in risk or return is obtained by diversification. Now assume that there is a zero correlation between the returns of A and B. This can be symbolically represented by returns for four periods:

CASE 1

Asset	Year 1	Year 2	Year 3	Year 4
A	+30	+30	-10	-10
B	+30	-10	+30	-10
Equal Mix	+30	+10	+10	-10

This example yields an annualized return of 9.0794%, and a standard deviation of 14.142%. The standard deviation of the portfolio has been reduced by a factor of the square root of 2 (and the variance halved) as predicted by Markowitz. However, the return is 0.9129% higher than the Markowitz return. Further, this excess return would not have been realized without rebalancing. This portfolio thus has a "rebalancing bonus" (hereafter known as the "RB") of 0.9129%. If instead the returns on A and B are perfectly inversely correlated (r = -1) it can be seen that the return of the portfolio each year will be 10%, as will be the annualized return, and the standard deviation and variance zero. The RB will thus be 1.8355% in this highly theoretical instance, which is slightly more than twice the bonus in the instance where r =0. Simple inspection suggests that the RB is proportional to:

Assume that the returns on asset A are still +30 and -10, but that now the return on B can be either +15 or +5. Asset B then has an expected return of 9.8863%(and a standard deviation of 10%; one half of the SD of asset A). The Markowitz return for a 50/50 mixture of A and B is 9.0264% (the average of 8.1665% and 9.8863%).

For the r =0 uncorrelated example:

Case 2

Asset	Year 1	Year 2	Year 3	Year 4
A	+30	+30	-10	-10
B	+15	+5	+15	+5
Equal Mix	+22.5	+17.5	+2.5	-2.5

Here, the annualized return is 9.5155%, yielding an RB of 0.4891%, or about one half of the uncorrelated example in case 1. Further experimentation demonstrates that the rebalancing bonus of any combination of two assets is roughly approximated by the expression:

where SD₁ is the standard deviation of asset 1, X₁ is the amount of asset 1.

Taking this process one step further, consider the case where an asset with returns of either +30 or -10 is mixed with a riskless asset whose return is always zero. The return on a 50/50 mix of these two assets will be either +15 or -5. The Markowitz return of this mix is 4.0833% (the mean of 8.1665 and zero), but it's actual return is 4.5227%, yielding an RB of 0.4394%. Since the standard deviation of the riskless asset is zero, the expression derived above will equal zero also, so an additional term is needed. A bit more experimentation shows that this term can be closely approximated by:

Thus, it is postulated that the "theoretical RB," RB_1,2, can be expressed as:

or more simply,

Stated succinctly, the intrinsic rebalancing potential of any asset pair is the difference between its mean variance and covariance. The above formulation was tested for 50/50 mixtures of asset pairs of the below assets:⁵

S&P 500 index
MCSI-EAFE
US 9-10 portfolio (DFA US small co. portfolio)
Equity REIT(NAREIT index)
MSCI-EAFE Europe
MSCI-EAFE Pacific
MSCI-EAFE Emerging Markets
UK small stocks(DFA UK small co. portfolio)
Japanese small stocks(DFA Japanese small co. portfolio)
Continental European small stocks(DFA Continental small co. portfolio)
Precious Metals(Morningstar fund index)
Natural Resources(Morningstar fund index)
Lehman Long Term Government Index
International Bond(Morningstar fund index)
One year corporate notes(DFA one year fixed fund)

The theoretical RB was calculated from SDs and correlation coefficients derived from quarterly data for the period July 1988 to December 1994. Similarly, the "actual" portfolios were rebalanced quarterly. A linear correction was applied to each series of quarterly returns to yield a zero annualized return for each individual asset over the whole study period; thus any return obtained from the asset pair must be due to rebalancing.

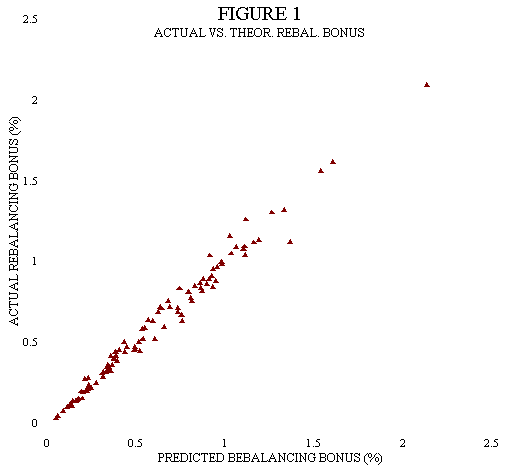
The 105 resultant theoretical/actual data points for each asset pair were plotted in Figure 1. As is seen, the theoretical data is highly predictive of the actual data, with an R² of 0.983 and a standard error of 0.052% of yield.

To summarize thus far: The beneficial effect of poorly correlated assets on portfolio risk, undoubtedly appreciated since antiquity, was mathematically formalized only forty years ago by Markowitz. The above theoretical model and backtested portfolios suggest that significant excess return is available from combinations of asset pairs which have both low correlation and high risk.

The capital asset pricing model asserts that the "risky" portion of one's portfolio should be a capitalization weighted "market portfolio" of all the world's investible risky assets.³ The above considerations provide an argument against portfolio capitalization weighting, since by definition capitalization weighting denies the need for rebalancing. Assets and sectors which have been battered or inflated will find their capitalization weighting commensurately reduced or increased. Consider the MSCI-EAFE index. During the study period July 1988 to December 1994 the US investor passively employing this index saw their percentage of Japanese holdings increase and decrease precipitously. On the other hand, the investor who kept his or her foreign assets equally divided between the European and Pacific sides of this index reaped an excess return of 0.588% for the period studied, with a modest concomitant reduction in risk. The emerging markets provide an even more vivid example of this phenomenon. The Latin American and Far Eastern components of the MSCI-EAFE EM index have very high standard deviations and are imperfectly correlated. The above model suggests that the investor who actively rebalances these two sectors will reap an advantage of at least two or three percent over their passively invested colleague. It seems highly likely that adherence to fixed percentage allocations among finely divided market sectors offers significant advantages over a passive market portfolio/market capitalization approach.

FREQUENCY OF REBALANCING

Although the need for portfolio rebalancing to policy composition is generally acknowledged, scant attention has been paid to it's frequency. In a rare paper addressing this issue, Arnott and Lovell ⁴ found that for the years 1968-91 a 50/50 stock/bond mix produced a return of 9.02% for annual rebalancing, 9.12% for quarterly rebalancing, and 9.16% for monthly rebalancing. Trading costs reduced the rebalancing benefit slightly, but even monthly rebalancing was still of benefit after transaction costs were considered. They also found that nonperiodic "threshold rebalancing" when portfolio composition surpassed 1%, 2%, and 5% excess/deficiency produced somewhat lesser gains. They surmised "Over this period, regular monthly rebalancing returns dominated less active approaches. Should one infer that daily rebalancing is better still? One cannot say, but it seems plausible."

The above formulation provides a framework for further investigation of the rebalancing frequency problem. One can calculate a "theoretical rebalancing bonus" for each of the different periods. It is well known that asset return correlations vary somewhat over time. It is less well appreciated that the individual return standard deviations and paired correlation coefficients are not the same for differing sampling intervals within the same epoch. For a given historical epoch the standard deviation of returns of a single asset may be different for shorter or longer measuring intervals. Even larger differences may be present for correlation coefficients of asset pairs. To illustrate this point, and to provide a basis for further discussion, I have provided standard deviation and correlation data for five different assets for monthly, quarterly, and annual returns in Table 1: UK, Japanese, Continental, and US 9-10 decile small stocks, and the MSCI-Emerging Markets Index, again for the July 1988-December 1994 period. These particular assets were chosen because of their low mutual correlations and high return standard deviations.

Next, "actual" or "observed" RBs for the resultant 10 asset pairs were calculated for monthly, quarterly, and annual rebalancing, and compared to the "theoretical," or "predicted" value. The data are presented in Table 2.

Table 1

	Standard Deviation(%)	CONT SM	JAP SM	MSCI-EM	US SM	UK SM
CONT SM	m: 14.54 q: 15.87 a: 19.86	m: 1.000 q: 1.000 a: 1.000
JAP SM	m: 32.29 q: 28.57 a: 24.63	m: .539 q: .483 a: .798	m: 1.000 q: 1.000 a: 1.000
MSCI-EM	m: 22.57 q: 27.06 a: 30.96	m: .154 q: .123 a: .634	m: .244 q: -.098 a: .653	m: 1.000 q: 1.000 a: 1.000
US SM	m: 14.71 q: 18.25 a: 19.50	m: .099 q: .007 a: -.154	m: .156 q: .217 a: .242	m: .379 q: .552 a: .590	m: 1.000 q: 1.000 a: 1.000
UK SM	m: 19.91 q: 17.79 a: 13.82	m: .620 q: .478 a: .251	m: .541 q: .478 a: .378	m: .305 q: .158 a: .614	m: .302 q: .309 a: .424	m: 1.000 q: 1.000 a: 1.000

(m=monthly, q=quarterly, a=annual All SDs are annualized, calculated as twice the quaterly SD, and 3.4641 times the monthly SD)

Table 2

Asset Pair	Monthly RB actual/predicted	Quarterly RB actual/predicted	Annual RB actual/predicted
CONT SM/JAP SM	0.911/0.871	0.818/0.787	0.345/0.275
CONT SM/MSCI-EM	0.788/0.778	1.099/1.102	0.941/0.717
CONT SM/US SM	0.484/0.482	0.694/0.762	1.171/1.118
CONT SM/UK SM	0.311/0.311	0.412/0.369	0.529/0.551
JAP SM/MSCI-EM	1.455/1.469	2.099/2.125	0.681/0.712
JAP SM/US SM	1.347/1.388	1.124/1.153	0.929/0.943
JAP SM/UK SM	0.917/0.930	0.885/0.940	0.710/0.678
MSCI-EM/US SM	0.591/0.592	0.600/0.650	0.705/0.783
MSCI-EM/UK SM	0.787/0.790	1.267/1.109	0.987/0.779
UK SM/US SM	0.541/0.545	0.644/0.651	0.477/0.428

These data make three main points:

1) No one rebalancing period dominates. Monthly rebalancing was best in three cases, quarterly in four, and annual in three.

2) The theoretical RB was highly predictive in all cases where significantly different rebalancing bonuses were obtained with different intervals. Only in three instances were minor (<0.05%) ranking errors made. Further, in cases where significant advantage is gained by the use of a particular rebalancing period complex calculations are not necessary. For example, referring to Table 2, it can be seen that for the pair Jap./EM, quarterly rebalancing is clearly superior to monthly or annual rebalancing. This is reflected nicely in the predicted values, and in table 1 it can be seen that this is primarily because the quarterly correlation coefficient is significantly lower than the monthly or annual values.

3) Those who rely on optimization procedures must be cognizant of the sampling interval used to calculate the standard deviation and correlation input data. Optimization outputs are liable to be very different for data obtained from monthly, quaterly, and annual sampling from within the same historical period.

Obviously, real portfolios are far more complex than asset pairs. It seems reasonable to assume that, analogous to the Markowitz formula for portfolio variance, the formula for a portfolio RB can be represented by:

(Each term for which i=j will be zero.) Applying this formula to an equal mix (20% each) of the five assets used above yields an observed/predicted RB of 1.205/1.118% for annual, 1.542/1.556% for quarterly, and 1.304/1.301% for monthly rebalancing. The annualized portfolio SDs are 16.80% for annual, 13.65% for quarterly, and 14.55% for monthly rebalancing--the same preference ranking as for the RB. This should not be surprising as asset pair covariance is the dominant component for both portfolio RB and portfolio variance for porfolios where n>2. Further work is necessary to evaluate the value of this formula for the estimation of rebalancing benefit for more complex portfolios. It may transpire that the complex relationship between pair correlations and single asset standard deviations measured over shorter or longer time period lengths will not be stable enough to render ex post analysis of much value.

PRECIOUS METALS STOCKS -- A SPECIAL CASE

The portfolio characteristics of precious metals equity are unique; very low long term return, very high return variance, and near zero correlation with most other asset classes. One of the primary rationales for this behavior is that most of the risk of this asset class is nonsystematic because of its low correlation with other assets -- in other words, it can be diversified away. The above discussion provides another perspective on this paradox. Examination of the theoretical rebalancing formula shows that the addition of a small amount of a high variance zero correlating asset to a portfolio with a much lower variance increases its apparent return by approximately one half of its variance. In other words, since the variance of a typical portfolio of precious metals stocks is about 0.1, its apparent return (IRR) in a rebalanced portfolio will be about 5% higher than its long term stand alone return. This is precisely what is observed by the investor who periodically rebalances the precious metals component of their portfolio as a fixed proportion; a large fraction of the IRR of this component comes from rebalancing per se. Thus, not only is the systematic risk of precioius metals stocks much lower than its stand alone risk, but its rebalanced portfolio return is much higher than its observed stand alone long term return.

CONCLUSIONS:

1. The expected return of a rebalanced portfolio is not accurately represented by simple arithmetic weighting of individual asset returns. This is particularly true of assets which have high standard deviations and are poorly correlated. This may be of some importance to those utilizing optimization technology which depends on linear expected return determinations. Standard MVO techniques underestimate the benefit of high variance/low correlation assets.

2. The capitalization weighting suggested by the CAPM does not appear to be maximally efficient.

3. A formula is presented which accurately predicts rebalancing benefit. The inputs to this equation are portfolio composition, individual asset standard deviation/variance, and asset pair correlation/covariance. Since these parameters vary with sampling interval, it may be possible to use this formula to predict the optimal rebalancing frequency. Further, the results of the analyses presented suggest that shorter rebalancing intervals may not always be optimal.

4. Optimizers should understand that sampling interval will significantly affect both input and output data, and that he or she is optimizing only for standard deviatons (or other risk measures, such as semivariance) over a given sampling interval.

REFERENCES

1. Harry M. Markowitz, Portfolio Selection: Efficient Diversification of Investments 2nd ed. (Cambridge, Massachusetts: Basil Blackwell Ltd., 1991), 67.

2. Andre F. Perold and William F. Sharpe, "Dynamic Strategies for Asset Allocation" Financial Analysts Journal (January/February 1988):16-27.

3. Roger G. Ibbotson and Gary P. Brinson, Global Investing: the Professional's Guide to the World Capital Markets (New York: McGraw Hill Inc., 1992), 43-44.

4. Robert D. Arnott and Robert M. Lovell, "Rebalancing: Why? When? How Often?" The Journal of Investing 2, no. 1 (Spring 1993): 5.

5. US stock and bond returns from Stocks, Bonds, Bills and Inflation 1995 Yearbook, Ibbotson Associates, Inc., Chicago. The 1988-94 quarterly returns data were obtained from Principia for closed and open end funds from Morningstar Associates, Chicago.

William J. Bernstein
wbern@mail.coos.or.us

copyright (c) 1996, William J. Bernstein