CHAPTER ONE
General Considerations
Imagine that you work for your rich but eccentric Uncle Fred. He is a conscientious and kind employer, and after some years in his service he decides to let you in on the company pension plan. You are 30 years old and will work for your uncle until you retire in 35 years at age 65. Each year he will contribute $5000 to your retirement account. Further, you must pick ahead of time one of two investment choices for the duration of your employment:
1. Certificates of deposit with a 3% annualized rate of return, or,
2. A most peculiar option: At the end of each year Uncle Fred flips a coin. Heads you receive a 30% investment return for that year, tails a minus 10% (loss) for the year. This will be hereafter referred to as "Uncle Fred’s coin toss," or simply, the "coin toss."
The first choice gives you a fixed rate of return, and in fact an absolutely certain lump sum at the end of your 35 years. You are adept with a financial calculator, and in a few seconds determine that this option will yield a sum of $302,310 with which to support your golden years. You realize that inflation will diminish the future value of this princely sum. In fact, if inflation is also 3%, you will be left with only $107,436 of current spending power.
The second choice confuses you at first. The thought of losing 10% of your hard-earned retirement money with the toss of a coin is too much to bear. What if you have a string of losing years? If you get tails all 35 years, you could be left with only a pittance for your retirement. On the other hand, if you get heads all 35 years you know that you will bankrupt poor Uncle Fred with your gains—he will owe you $162,000,000!
Let’s look a bit more closely at the second choice. Over a long enough period, you will get exactly half heads and half tails. If you represent this with an alternating series of heads and tails, then your return in each 2-year period is represented by:
1.3 X 0.9 = 1.17
(The first year return of 30% results in your account being multiplied by 1.3, while a 10% loss multiplies your sum by 0.9. For each dollar you had at the beginning of the 2-year period, you now have $1.17.)
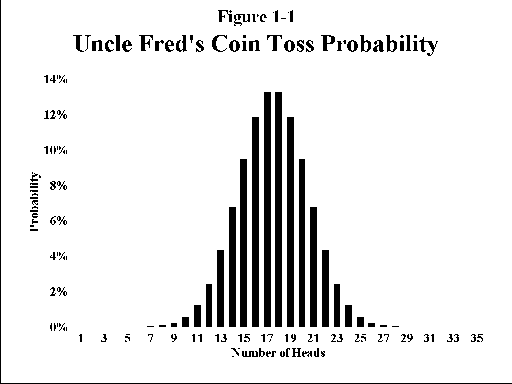
You again get out your calculator and find that a 17% return at the end of 2 years is the same as an annual return of 8.17%. This is clearly superior to the 3% return of the first option. Of course, you could have a string of bad luck and get tails more than half of the time. However, with some trial and error on your calculator you discover that you would have to get 12 heads and 23 tails before you come out worse than the first option, and you decide that the odds of this are quite low. You visit your former college statistics professor, who chides you for forgetting that you could have easily calculated the odds of any combination of coin flips with the so-called "binomial distribution function." The blank look elicits a sigh from him, he heads over to his computer, pulls up a spreadsheet program, and after a few keystrokes hands you the graph in Figure 1-1:

The coin toss also introduces the difference between the average and the annualized return of an asset. Some of you may wonder why the return of the coin toss is not 10% instead of 8.17%, since the average of +30% and -10% is +10%. (30 minus 10, divided by 2). The average return is simply the average of each of the individual annual returns. The annualized return is a more subtle concept. It is the return that you must earn each and every year to equal the result of your series of differing annual returns. If you own a stock which doubles (has a 100% return) the first year and then loses 50% the next year you have a zero annualized return. Since the stock was worth 10 dollars per share at the start, it was worth 20 dollars at the end of the first year, and 10 dollars again at the end of the second year. You have made no money, and yet the average return is "25%" (the average of +100% and -50%). Your annualized return is zero. The annualized and average return clearly are not the same. The coin toss has an average return of 10%, and an annualized return of 8.17%. The annualized return is always less than the average return. If in the coin toss you come up with half -10% and half +30% returns, this is the same as having an 8.17% return each and every year. You pay your bills with annualized return, not average return. This is why annualized returns are so important.
Uncle Fred’s coin toss may seem a most bizarre scenario, and yet it is nearly identical to the choice faced by most investors between the "safety" of money market accounts/treasury bills and the "gamble" of common stocks. The second option offers a near certainty of a superior result, yet comes at a price: the small possibility of an inferior result and, more importantly, that gut wrenching coin toss session with Uncle Fred each year. And yet, it is the 3% certificate of deposit option which is the most truly frightening—you will almost certainly live your golden years in poverty.
I constructed Uncle Fred’s coin toss with some deliberation—it’s easy to grasp and quite closely approximates the returns and risks of common stocks. The return of common stocks over the past 73 years (1926-98) was 11.22%, in the same league as the coin toss. More importantly, the "riskiness" of the coin toss and of common stocks is nearly identical. I shall explain shortly how to measure precisely this riskiness. The coin toss is a handy symbolic representation of the risks and returns of common stocks. It will also provide a powerful way in which to understand the behavior of portfolios with multiple asset types.
You have just been introduced to one of the fundamental laws of investing: in the long run you are compensated for bearing risk. Conversely, if you seek safety, your returns will be low. Experienced investors understand that reward and risk are inextricably intertwined; one of the most reliable ways to spot investment fraud is the promise of excessive returns with low risk.
Let’s consider an example of investment return slightly more complex than the coin toss. Say that you have invested in security A (it doesn’t matter what it is). The returns for eight consecutive years are as follows:
Year 1: 20%
Year 2: 0%
Year 3: 10%
Year 4: -10%
Year 5: 30%
Year 6: 15%
Year 7: 10%
Year 8: 5%
What is your return on security A? In the year that your return was 30% you have multiplied your asset value by 1.3, for 0% you multiply by 1.0, for -5% you multiply by 0.95, etc. Thus, over the full eight years your final value is calculated as:
1.2 x 1.0 x 1.1 x 0.9 x 1.3 x 1.15 x 1.1 x 1.05 = 2.051
In this example, if security A was worth $10 at the beginning of the period, it is now worth 2.051 times the original value, $20.51. The total return over 8 years is 105.1% (Don’t be confused by this; remember that a gain of 50% means multiplying your initial amount by 1.5, and that a gain of 100% means multiplying by 2.) The average return is simply the average of the 8 individual returns, or 10%. However, we know that what really counts is the annualized return (that is, the return which would be required each year to yield the same result). How do we calculate this? If you are familiar with spreadsheets this is a snap—all spreadsheet packages have extensive financial calculation capability. If you are unfamiliar with spreadsheets, then the easiest way to do this is with a financial calculator. If you do not own one, you should. The Texas Instrument BA-35, or its equivalent, can be found in almost any large drug or general merchandise store. It should cost about $20. I urge you to learn how to use the annuity features on this or a similar device—you will find it indispensable for planning your retirement, calculating loan payments, etc. This calculator also has a statistical function that will enable you to rapidly calculate investment risk from a series of returns. Plugging the numbers into the annuity function, we find that the annualized return for the above example is 9.397%. It should not surprise you that this is slightly less than the 10% average return, since annualized return is always less than average return.
We are now ready to calculate the risk of security A. This is done by calculating a standard deviation, or "SD." SD is a measure of the "scatter" of a set of numbers. Its calculation can be done by hand, but this is quite tedious. Again, this is typically done with a spreadsheet or financial calculator. In the case of the above 8 returns, the SD was 11.46%.
What do you do with a standard deviation? First and foremost, you should become familiar with this as a measure of risk. Typically, the standard deviation of the annual returns for various asset classes are as follows:
Money market (cash): 2%-3%
Short-term bond: 3%-5%
Long bond: 6%-8%
Domestic stocks (conservative): 10-14%
Domestic stocks (aggressive): 15%-25%
Foreign stocks: 15%-25%
Emerging Markets stocks: 25%-35%
Almost all of the mutual fund rating services list this statistic in their reports. Morningstar Inc., a company which compiles information about and analyzes mutual funds, lists standard deviations of annual returns for the preceding 3, 5, and10 years. In some cases you may have returns for only a year or two. Here the standard deviation of annual returns may be estimated by multiplying the quarterly returns SD by 2 or the monthly returns SD by 3.46. Anytime a salesman or broker attempts to sell you a security of any type, ask him or her what its standard deviation of annual returns is (or is expected to be if it is a new offering). If he or she doesn’t know, don’t even think about buying it. If your broker is not familiar with the concept of the standard deviation of returns, get a new one.
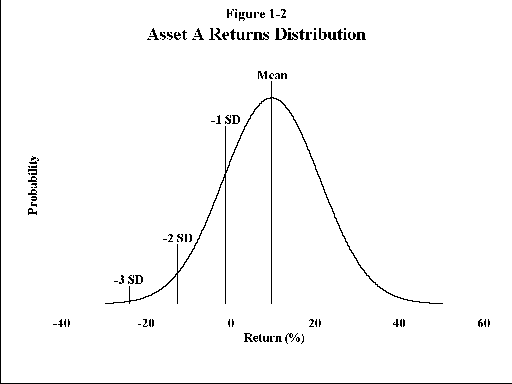
What does the standard deviation number actually mean? It means that two thirds of the time the annual return of the asset will lie between 1 standard deviation above and 1 standard deviation below the mean value. In the case of security A this means that two thirds of the time it will be between -1.46% (10 minus 11.46) and 21.46% (10 plus 11.46). I've graphed the "downside" for security A in Figure 1-2:
OTHER MEASURES OF RISK
Those of you with sophisticated math backgrounds will recognize the limitations of SD as a measure of risk. For example, in the real world of investing, returns do not follow a classic "normal distribution," but instead more closely approximate a "lognormal" distribution. Further, there is a degree of asymmetry about the mean ("skew") as well as a somewhat higher frequency of events at the extremes of range ("kurtosis"). The most important criticism of standard deviation as a measure of risk is that it assigns equal importance to returns both above as well as below the mean, whereas clearly only events occurring below the mean are of importance to any measurement of investment risk. This has prompted some academics and practitioners to suggest "semivariance," or the mean variance of events occurring below the mean, as a more realistic measurement of risk. In practice, however, both variance and semivariance yield very similar results, and variance/standard deviation is still an excellent measure of risk. In fact, simple variance/SD has the additional advantage of giving you two chances of catching excessive volatility. In the recent notorious case of Long Term Capital Management, the firm did not develop a significantly negative semivariance until shortly before bankruptcy. Simple calculation of the plain vanilla SD/variance of monthly returns would have warned of trouble years before the ottoman hit the fan.
There are nearly as many definitions of risk as there are finance academics. Other possible measures include the probability of a nominal loss, or an inflation adjusted loss, a "loss standard deviation," or the probability of underperforming a given index, such as the S&P 500 or T-bill yield. A measure favored by many is the probability that your investment will underperform a risk free asset, usually T-bills. This is easily calculated from a formula using a "standard normal cumulative distribution function," the one used by your hypothetical statistics professor. You can easily make up your own. Such individual measures of risk and return are referred to as "utility functions."
If you have digested all of the material in this chapter thus far, you have either worked very hard or you are good with numbers (or have had a course in statistics). Take the rest of the day off, sit by the pool, have a Margarita. You’ve earned it. When you return, we shall begin our consideration of real assets.
copyright (c) 1999, William J. Bernstein